在很多人看来数学和艺术这两个东西似乎不太沾边,但其实二者的关系颇为微妙。这两个分属不同学科,一个表现抽象概念,另一个则注重感官与情感表达。然而两者互相的作用与促进却从来没有间断过。
我们都知道通过数学,通过公式的演算,能够构成非常奇妙的艺术观感与审美,在实际生活中这种运用的例子也随处可见。
1,斐波那契螺旋线
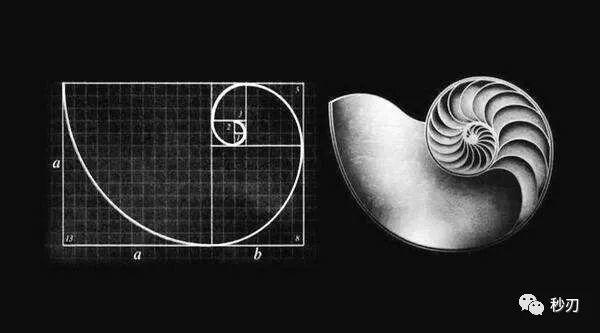
也称“黄金螺旋”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个90度的扇形,连起来的弧线就是斐波那契螺旋线。它来 源于斐波那契数列(FibonacciSequence),又称为黄金分割数列。

建筑邻域的运用
2,皮亚诺曲线
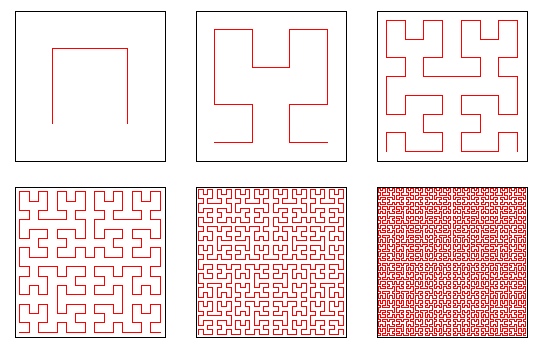
皮亚诺(Peano)曲线是一条能够填满正方形的曲线。在传统概念中,曲线的数维是1维, 正方形是2维。1890年,意大利数学家皮亚诺(Peano G)发明能填满一个正方形的曲线,叫做皮亚诺曲线。

似乎是根据其灵感来源设计的柜子
3,莫比乌斯环

由德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现:把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。


实际邻域中的一些近似应用
4,黄金矩形
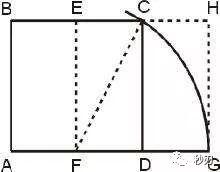
黄金矩形(Golden Rectangle)的长宽之比为黄金分割率,换言之,矩形的短边为长边的 0.618倍 [1] 。黄金分割率和黄金矩形能够给画面带来美感,令人愉悦。在很多艺术品以及大自然中都能找到它,希腊雅典的巴特农神庙就是一个很好的例子。蒙娜丽莎的脸符合黄金矩形,同样也应用了该比例布局。


5,分形
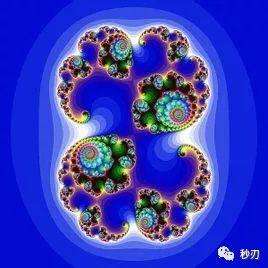
具有以非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。
它们在不同尺度下不断重复所形成的图案,无限地创造着那些我们平时常见的如线条、曲线、漩涡等等各种图案。英国物理学家汤姆·贝达德 (Tom Beddard) 用数字技术呈现了3D版法贝热彩蛋 (Fabergé egg),彩蛋上就覆盖着这种分形图案。


“这些3D分形由迭代方程而来,每个迭代方程的输出结果即为下一个方程的输入项。”贝达德介绍,“方程能够有效地进行折叠、缩放、翻转等等。这是很奇妙的分形艺术,你越贴近表面去观察,越能看到更多的精彩细节。”
由上面一些介绍您大概可以了解数学在艺术领域的应用已经非常之广亦或者说无处不在。那么下面的一些例子似乎是截然相反的。
1,阿尔罕布拉宫的图案



14世纪和15世纪柏柏尔人君主的宫殿和寝宫——阿尔罕布拉宫。拥有诸多喷泉的楼天庭院,遮阴避雨的环廊。天花板上布满了类似钟乳石的精美几何图案。精美的四周墙壁的多彩瓷砖上的装饰,令人眼花缭乱。这种装饰方法利用规则的几何图形覆盖整个空间。数学上已证实,平面能够被三角形、四边形和六边形等图形铺满,几种图案相互拼凑也可以,但唯独五边形不行。这种精美的几何组合,使得看起来并不像静止,而是有一种莫名的动感。

在数学家们已经鉴定出17种对称形中,阿尔罕布拉宫就包含了至少16种。这些图案不仅漂亮,还有着严密的数学逻辑,几乎完全囊括了基本的对称特性。而数学家们直到阿尔罕布拉宫建成几个世纪之后才提出对称原理的分析。
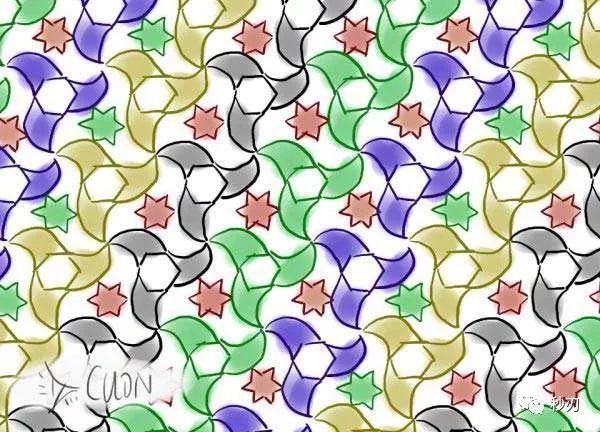
2,准晶体图案

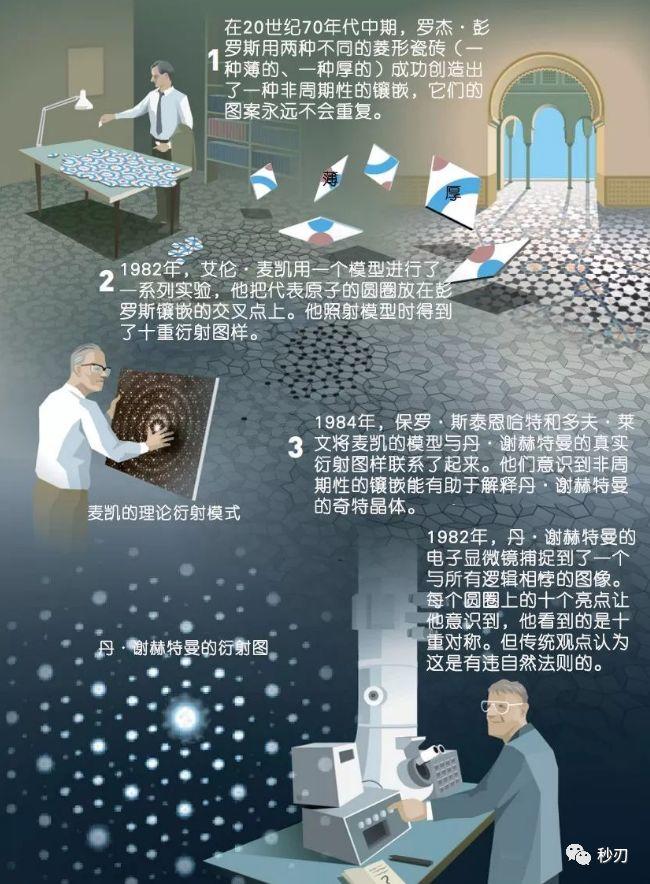
这种图形最大的特点在于能以规则的形状完全填满空间,但是所用的图形绝不重复。然而最初发现这种图案的是早在1453年,一个伊斯法罕Darbi-I Imam圣地的无名工匠。这些图形具有复杂神秘的数学性质,直到1970年代彭罗斯拼图的发现,数学家才能够进行分析。
3,透视和非欧几里德数学

在文艺复兴时期,艺术得到了飞速的发展,而几何透视更引发了其艺术变革,按照当时的理解,两条平行的直线最终会相交于所谓的“没影点”。文艺复兴透视提出了一种遵循通常数学法则的几何。
数学家在 19 世纪初首次构想出非欧几里得数学时,他们设想了一个平行线会在无限远处相交的世界。他们探索的几何学在很多方面与文艺复兴时期的透视法相似。
从那以后,非欧几里得数学开始探索 12、13 维的空间,这远远超出了文艺复兴时期的透视法。但值得思考的是,文艺复兴时期的艺术是否让最初的这步飞跃变得更加容易了?
4,波洛克的混乱画作

杰克逊·波洛克(1912-1956)处于抽象表现主义的最前沿,他在1947-1950年创立的滴画风格,一直是名人和评论界的关注点。在这些颇具革命性的作品中,波洛克把未完全撑开的画布平铺在画室地面,然后将房屋用的珐琅颜料倾倒、滴注上去。这样形成的视觉效果,用波洛克自己的话说,是“让人能看到的能量和动作”的旋风。

这是他最出名的画作——《薰衣草之雾》
当然这不是作者自己的命名,波洛克只用数字和日期为这些滴画起名。评论家克莱门特·格林伯格(Clement Greenberg)将这幅作品命名为“薰衣草之雾”,尽管实际上没有使用薰衣草色,但灰色、棕土色和暗黑的玫瑰色创造出虚无缥缈的色调,仿佛某种光环。波洛克将自己的手印围绕在构图的外围边缘。这些记号是他在图像中真实存在的信号,强调出画作表面的平整。相对而言,无数串颜料似乎表达出无限之感,甚至让人想起宇宙空间的流动。
他的画作让人琢磨不透,起初看上去似乎杂乱无章,但随着时间推移,我们会逐渐发现其中具有一定的有序元素。




它们的形状既可预测又不可预测,就像水龙头的滴水模式一样,你无法预测下一次水滴的确切效果。但是,如果我们绘制滴水的图案,就会发现会落入一个具有清晰形状和边界的区域。
然而波洛克本人对数学却没有任何特别的兴趣,他所创造出的这些迷人的形式都是出于直觉和主观。虽然众多数学家至今无法解读他的作品,但波洛克的同时混乱和有序的图形仍然为数学研究提供了多种可能的方向。
由此可见,艺术和数学两者的相互影响,让人不能完全的断定是哪一边起的作用更大,到底是艺术促进了数学的发展,还是通过数学展现并解读了艺术更多的可能性,这都不重要,重要的是它们都是人类历史发展上的瑰宝。
(图片及部分文字来自网络)
新年了,想说的很多,但什么都不想说,望各位保重。
